模型展示:角“8”字型
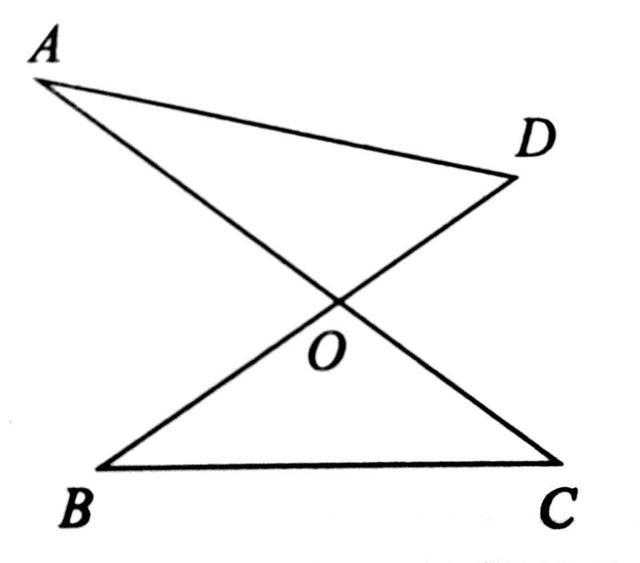
如图所示:AC、BD相交于O,连接AD、BC,则:∠A+∠D=∠B+∠C,
注:(1)因为图形像“8”,故而称为“8”字型。(2)“8”字型通常在几何综合题中穿插使用
模型拆解证明:∵∠AOB是△AOD的外角度,
∴∠A+∠D=∠AOB。
又∵∠B+∠C=∠AOB
∴∠A+∠D=∠B+∠C
模型例证计算角度:
如图:∠A+∠B+∠C+∠D+∠E+∠F=()
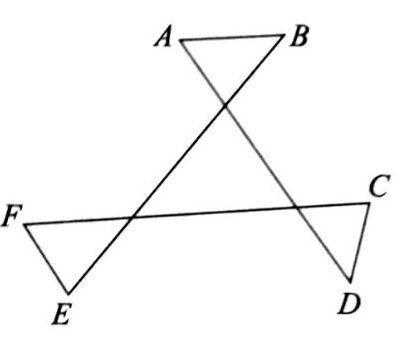
如图,连接DE.
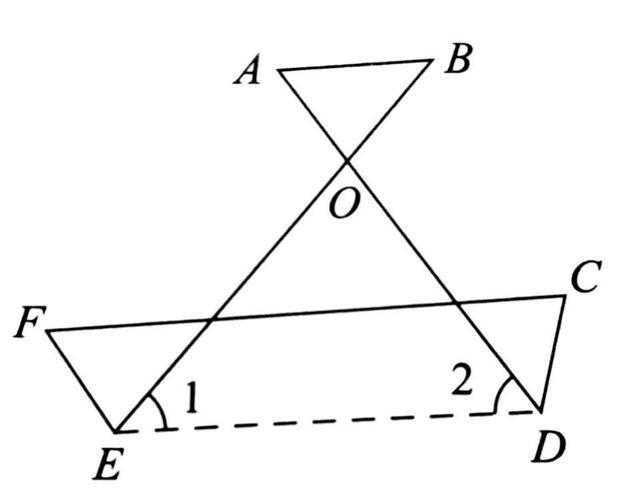
∴∠A+∠B=∠AOE
又∵∠AOE是△OED的外角,
∴∠1+∠2=∠AOE
∴∠A+∠B=∠1+∠2(角“8”字型)
∴∠A+∠B+∠C+∠ADC+∠FEB+∠F
=∠1+∠2+∠C+∠ADC+∠FEB+∠F
=360°
模型练习
如图,求∠CAD+∠B+∠C+∠D+∠E=()
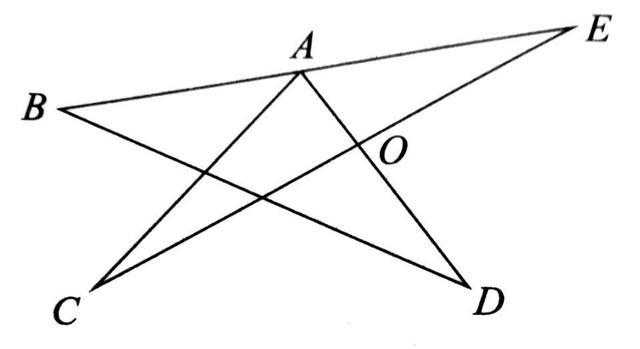
解答
方法一:如下图:
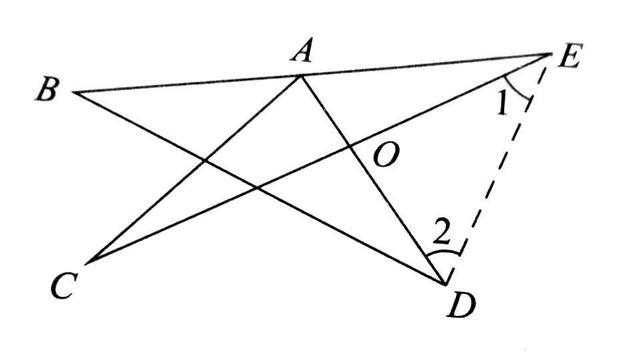
连接DE,
易得:∠C+∠CAD=∠1+∠2,(角“8”字型)
∴∠CAD+∠B+∠C+∠ADB+∠BEC
=∠B+∠BEC+∠BAD+∠1+∠2
=180°
方法二:如下图:
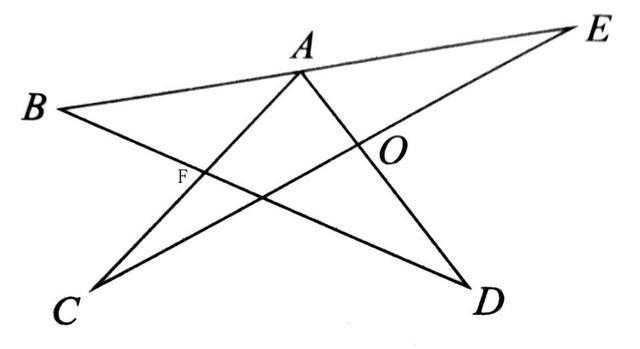
由三角形外角的性质,得:
∠C+∠E=∠BAC,∠CAD+∠D=∠AFB,
由三角形的内角和定理,得:
∠B+∠BAC+∠AFB=180°
等量代换,得:∠CAD+∠B+∠C+∠D+∠E=180°
举报/反馈
免责声明:本文章如果文章侵权,请联系我们处理,本站仅提供信息存储空间服务如因作品内容、版权和其他问题请于本站联系